DERIVADA DE UNA FUNCION
En matemáticas, la derivada de una función es una medida de la rapidez con la que cambia el valor de una función matemática, según cambie el valor de su variable independiente. La derivada de una función se calcula como el límite de la rapidez de cambio media de la función en un cierto intervalo, cuando el intervalo considerado para la variable independiente se torna cada vez más pequeño. Por ello se habla del valor de la derivada de una cierta función en un punto dado.
Entonces el valor de la derivada de una función en un punto puede interpretarse geométricamente, ya que se corresponde con la pendiente de la recta tangente a la gráfica de la función en dicho punto.
El concepto de derivada de una función matemática se halla íntimamente relacionado con la noción de límite. Así, la derivada se entiende como la variación que experimenta la función de forma instantánea, es decir, entre cada dos puntos de su dominio suficientemente próximos entre sí. La idea de instantaneidad que transmite la derivada posee múltiples aplicaciones en la descripción de los fenómenos científicos, tanto naturales como sociales.
Entonces el valor de la derivada de una función en un punto puede interpretarse geométricamente, ya que se corresponde con la pendiente de la recta tangente a la gráfica de la función en dicho punto.
El concepto de derivada de una función matemática se halla íntimamente relacionado con la noción de límite. Así, la derivada se entiende como la variación que experimenta la función de forma instantánea, es decir, entre cada dos puntos de su dominio suficientemente próximos entre sí. La idea de instantaneidad que transmite la derivada posee múltiples aplicaciones en la descripción de los fenómenos científicos, tanto naturales como sociales.
Se llama Criterio de la primera derivada al método utilizado frecuentemente en el calculo matematico para determinar los minimos y maxiomos relativos que pueden existir en una funcion mediante el uso de la primera derivada o derivada principal, donde se observa el cambio de signo, en un intervalo abierto señalado que contiene alpunto critico  .
.
 .
.
Teorema valor máximo y mínimo
"Sea  un punto crítico de una función
un punto crítico de una función  que es continua en un intervalo abierto
que es continua en un intervalo abierto  que contiene a
que contiene a  . Si
. Si  es derivable en el intervalo, excepto posiblemente en
es derivable en el intervalo, excepto posiblemente en  , entonces
, entonces  puedeclasificarlo como sigue."
puedeclasificarlo como sigue."
 un punto crítico de una función
un punto crítico de una función  que es continua en un intervalo abierto
que es continua en un intervalo abierto  que contiene a
que contiene a  . Si
. Si  es derivable en el intervalo, excepto posiblemente en
es derivable en el intervalo, excepto posiblemente en  , entonces
, entonces  puedeclasificarlo como sigue."
puedeclasificarlo como sigue." '
' cambia de positiva a negativa en
cambia de positiva a negativa en  , entonces
, entonces  tiene un máximo relativo en
tiene un máximo relativo en  .
.2. Si
 '
' cambia de negativa a positiva en
cambia de negativa a positiva en  , entonces
, entonces  tiene un mínimo relativo en
tiene un mínimo relativo en  .
.3. Si
 '
' es positiva en ambos lados de
es positiva en ambos lados de  o negativa en ambos lados de c, entonces
o negativa en ambos lados de c, entonces  no es ni un mínimo ni un máximo relativo.
no es ni un mínimo ni un máximo relativo.https://sites.google.com/site/calculodiferencialfgv/home/unidad-iii/puntos-criticos-y-valores-extremos
CRITERIO DE LA SEGUNDA DERIVADA
El Criterio o prueba de la segunda derivada es un teorema o método del calculo matematico en el que se utiliza la segunda derivada para efectuar una prueba simple correspondiente a los máximos y mínimos relativos.
Se basa en el hecho de que si la gráfica de una función  es convexa en un intervalo abierto que contiene a
es convexa en un intervalo abierto que contiene a  , y
, y  debe ser un mínimo relativo de
debe ser un mínimo relativo de  . De manera similar, si la gráfica de una función es cóncava hacia abajo en un intervalo abierto que contiene a
. De manera similar, si la gráfica de una función es cóncava hacia abajo en un intervalo abierto que contiene a  y
y  debe ser un máximo relativo de
debe ser un máximo relativo de  .
.
 es convexa en un intervalo abierto que contiene a
es convexa en un intervalo abierto que contiene a  , y
, y  debe ser un mínimo relativo de
debe ser un mínimo relativo de  . De manera similar, si la gráfica de una función es cóncava hacia abajo en un intervalo abierto que contiene a
. De manera similar, si la gráfica de una función es cóncava hacia abajo en un intervalo abierto que contiene a  y
y  debe ser un máximo relativo de
debe ser un máximo relativo de  .
.
Teorema
Sea  una función tal que
una función tal que  y la segunda derivada de
y la segunda derivada de  existe en un intervalo abierto que contiene a
existe en un intervalo abierto que contiene a 
 una función tal que
una función tal que  y la segunda derivada de
y la segunda derivada de  existe en un intervalo abierto que contiene a
existe en un intervalo abierto que contiene a 
- Si
 , entonces
, entonces  tiene un máximo relativo en
tiene un máximo relativo en  .
. - Si
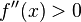 , entonces
, entonces  tiene un mínimo relativo en
tiene un mínimo relativo en  .
.
Si  , entonces el criterio falla. Esto es,
, entonces el criterio falla. Esto es,  quizás tenga un maximo relativo en
quizás tenga un maximo relativo en  , un mínimo relativo en
, un mínimo relativo en  o ninguno de los dos. Tomar como ejemplo lafuncion f(x) = x³. En tales casos, se puede utilizar el criterio de la primera derivada o el criterio de la tercera derivada.
o ninguno de los dos. Tomar como ejemplo lafuncion f(x) = x³. En tales casos, se puede utilizar el criterio de la primera derivada o el criterio de la tercera derivada.
 , entonces el criterio falla. Esto es,
, entonces el criterio falla. Esto es,  quizás tenga un maximo relativo en
quizás tenga un maximo relativo en  , un mínimo relativo en
, un mínimo relativo en  o ninguno de los dos. Tomar como ejemplo lafuncion f(x) = x³. En tales casos, se puede utilizar el criterio de la primera derivada o el criterio de la tercera derivada.
o ninguno de los dos. Tomar como ejemplo lafuncion f(x) = x³. En tales casos, se puede utilizar el criterio de la primera derivada o el criterio de la tercera derivada.
No hay comentarios:
Publicar un comentario